这篇笔记主要介绍死锁避免中的银行家算法的实现。同样是参考书上的例子和使用C++实现的。作为新年的第一篇文章🎉,我也尝试了一些新鲜的东西,比如Markdown中数学公式,同时为算法找了两个测试用例进行测试。
写文章耗时:1 hour
编码:1 hour
简介
死销避免动态地确定是否分配资源给提出请求的进程。如果一个进程当前请求资源会导致死锁,系统将拒绝启动此进程;如果一个资源分配会导致系统下一步死锁,便拒绝本次分配。
算法大师 Dijkstra 提出了银行家算法—一种死锁避免的实现:假定小城镇银行家拥有资金数量为∑,被N个客户共享,银行家对客户提出下列约束条件:每个客户必须预先说明所要的最大资金量;每个客户每次提出部分资金量的申请并获得分配;如果银行满足客户对资金的最大需求量,那么客户在资金运作后,应在有限时间内全部归还银行。
只要客户遵守上述约束条件,银行家将保证做到:若一个客户所要的最大资金量不超过∑,银行一定会接纳此客户并满足其资金需求;银行在收到一个客户的资金申请时,可能会因资金不足而让客户等待,但保证在有限时间内让客户获得资金。
在银行家算法中,客户可看做进程,资金可看做资源,银行家可看做操作系统。银行家算法虽然能避免死锁,但是在操作系统中实际应用时却很难实现,因为要求所涉及的进程不相交,即不能有同步要求,而且要知道进程的总数和每个进程请求的最大资源数,这些都很难办到。
既然很难实际应用,那么这个算法的意义何在?当然它现在对我来说最重要的意义就是应付考试😂;等到考试过去之后,我可能会说它的思想很重要,即使不能实际应用。
数据结构
对于一个拥有 n 个进程和 m 种不同资源的系统,定义以下的向量和矩阵:
- 系统中每类资源总数向量
Resource = [R1, R2, ..., Rm]
- 系统中每类资源当前可用数向量
Available = [V1, V2, ... ,Vm]
- 每个进程对各类资源的最大需求矩阵
Claim[i, j] = k,表示进程 P,需要 R 类资源的最大数目为 k 。
- 每个进程已占有各类资源数量矩阵
Allocation[i, j] = k示进程 P,已占用 R 类资源 k 个。
- 每个进程尚需各类资源数量矩阵
Need[i, j],若 Need[i, j] = k,表示进程P 需 R类资源k个。计算 Need 数组可以使用:Need[i, j]= Claim[i, j] -Allocation[i, j]
- 每个进程当前申请各类资源数量矩阵
Request[i, j] = k,表示进程 P 当前申请R类资源k个。
对应在 C++ 中的定义如下,在这里向量和矩阵其实就是一维数组和二维数组:
1
2
3
|
int resource[MAX_RESOURCE], available[MAX_RESOURCE];
int allocation[THREAD_NUM][MAX_RESOURCE];
int claim[THREAD_NUM][MAX_RESOURCE], need[THREAD_NUM][MAX_RESOURCE];
|
算法实现
当前系统状态是安全的,当且仅当存在一个进程序列 P0,P2,…,Pn-1,对进程 P(k=0, 2, …,n - 1)满足公式(第一次尝试在 Markdown 里写数学公式 🐱):
$$Need[k, i] ≤ Available[i] +\sum_{j=0}^{k-1}Allocation[j, i] (i = 0,…,m-1;k=1,…, n-1)$$
这个序列就称为安全序列。其中,公式左边表示进程P尚缺少的资源,$Available[i]$ 即 $V_i$ 是系统尚可用于分配且为P所想要的那类资源数,$Alocation[j, i]$ 表示排在进程 $P_k$ 之前的所有进程所占用的P所需要的资源总数。显然,进程P所需资源若不能立即被满足,那么在所有 $P_{j=0, 1,…,k-1}$ 运行完成后可以满足,然后 P 也能获得资源以完成任务;当 $P_k$ 释放全部资源后,$P_{k+1}$ 也能获得资源以完成任务。如此下去,直到最后一个进程完成任务,从该状态起按照这个进程序列运行的系统是安全的,所以不会产生死锁。
自然语言描述
银行家算法资源分配步骤如下:
*表示所有情况都满足这个等式/不等式,在代码中表示就是一个循环的事情
-
如果 Request[i, *] <= Need[i, *]转步骤2;否则,进程申请量超过最大需求量,拒绝请求。
-
如果 Request[i, *] <= Available[*],步骤3;否则,申请量超过当前系统所拥有的可分配量,拒绝请求,进程 P 等待。
-
系统对 P 进程请求资源进行试探性分配,执行
1
2
3
|
Allocation[i, *] = Allocation[i, *] + Request[i, *]
Available[*] = Available[*] - Request[i, *]
Need[i, *] = Need[i, *] - Request[i, *]
|
-
转向步骤5执行安全性测试算法,如果返回安全状态则承认试分配,否则抛弃试分配,进程P等待,并执行恢复原来的状态:
1
2
3
|
Allocation[i, *] = Allocation[i, *] - Request[i, *]
Available[*] = Available[*] + Request[i, *]
Need[i, *] = Need[i, *] + Request[i, *]
|
-
安全性测试算法
- 定义向量Work[i],布尔型标志 possible 和进程集合 rest;
- 执行初始化操作:让全部进程进入rest集合,并让:
Work[*] = Available[*]; possible=true;
- 保持
possible=true,从进程集合rest中找出满足下列条件的进程P:
Nee[k, *] <= work[*]
- 如果不存在,则转向5;如果找到,则释放进程P所占用的资源,并执行以下操作,假设现在 P 已经运行结束并释放资源:
Work[*] = Work[*] + Allocation[k, *]
把P从进程集合中去掉,再转向③;
- 置
possible = false,停止执行安全性测试;
- 最后查看进程集合rest,若其为空集则返回安全标记,否则返回不安全标记。
C++ 实现
安全性测试算法基本上和自然语言描述的步骤一致:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
|
/** Wether current state is safe.
* return true if safe, else return false.
* if return true, the safe_seq will be filled with the sequence that thread
* process
*/
bool is_safe(int *available, int need[][MAX_RESOURCE],
int alloction[][MAX_RESOURCE], int *safe_seq) {
int work[RESOURCE_NUM];
memcpy(work, available, sizeof(int) * RESOURCE_NUM);
set<int> rest;
set<int>::iterator it;
for (int i = 0; i < THREAD_NUM; i++) {
rest.insert(i);
}
int size = 0;
while (rest.size() != 0) {
// find a thread that its need < available
int id = -1;
bool no_possible = true;
for (it = rest.begin(); it != rest.end(); it++) {
bool ok = true;
for (int j = 0; j < RESOURCE_NUM; j++) {
if (need[*it][j] > work[j]) {
ok = false;
// break inner loop
j = RESOURCE_NUM;
}
}
if (ok) {
no_possible = false;
id = *it;
safe_seq[size++] = id;
// remove from set
rest.erase(it);
for (int k = 0; k < RESOURCE_NUM; k++) {
// assume we release this thread's resource
work[k] += alloction[*it][k];
}
break;
}
}
// no thread satisfied, stop search
if (no_possible) break;
}
return rest.size() == 0;
}
|
处理进程的资源请求:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
int thread_id;
int request[RESOURCE_NUM];
// input request thread id, index start from 0
while (scanf("%d", &thread_id) == 1) {
// input request
bool overflow = false;
for (int i = 0; i < RESOURCE_NUM; i++) {
scanf("%d", &request[i]);
if (request[i] > need[thread_id][i] || request[i] > available[i]) {
overflow = true;
printf("request rejected: request too much resource\n");
}
}
if (overflow) continue;
// try to satisfy request
for (int i = 0; i < RESOURCE_NUM; i++) {
allocation[thread_id][i] += request[i];
available[i] -= request[i];
need[thread_id][i] -= request[i];
}
printf("try to satisfy request, now available:\n");
print_sequence(available, RESOURCE_NUM);
if (is_safe(available, need, allocation, safe_sequence)) {
printf("request accepted\n");
} else {
printf("request rejected: state not safe\n");
// restore previous state
for (int i = 0; i < RESOURCE_NUM; i++) {
allocation[thread_id][i] -= request[i];
available[i] += request[i];
need[thread_id][i] += request[i];
}
}
}
|
完整的代码可以在我的 Gist 上查看。
测试用例
我分别用书上的例子和 wiki 上的例子来测试这个算法。
Test Case 1
1
2
3
|
Total system resources are:
A B C
10 5 7
|
1
2
3
|
Available system resources are:
A B C
3 3 2
|
1
2
3
4
5
6
7
|
Processes (currently allocated resources):
A B C
P0 0 1 0
P1 2 0 0
P2 3 0 2
P3 2 1 1
P4 0 0 2
|
1
2
3
4
5
6
7
|
Processes (maximum resources):
A B C
P0 7 5 3
P1 3 2 2
P2 9 0 2
P3 2 2 2
P4 4 3 3
|

请求:
1
2
3
|
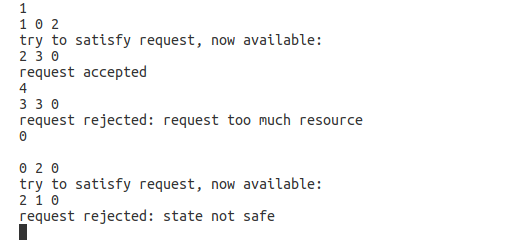
1. P1: 1 0 2
2. P4: 3 3 0
3. P0: 0 2 0
|
Test Case 2
1
2
3
|
Total system resources are:
A B C D
6 5 7 6
|
1
2
3
|
Available system resources are:
A B C D
3 1 1 2
|
1
2
3
4
5
|
Processes (currently allocated resources):
A B C D
P0 1 2 2 1
P1 1 0 3 3
P2 1 2 1 0
|
1
2
3
4
5
|
Processes (maximum resources):
A B C D
P0 3 3 2 2
P1 1 2 3 4
P2 1 3 5 0
|

参考


