最近在复习操作系统，老师不讲设备管理这一部分，让我们自学，期末要考电梯调度算法。这篇文章分别用自然语言，流程图，C++语言来描述电梯算法，其实电梯算法真的很简单😸

背景介绍

在介绍电梯算法之前，我们需要了解一下，它出现的背景，它是为了解决什么问题？

前面已经说过，这是设备管理的内容。对于电梯算法来说，它所管理的设备就是磁盘，而且是机械硬盘。硬盘的基本结构如下图，这里需要搞清几个概念：盘面、柱面、磁道、扇区、磁头：

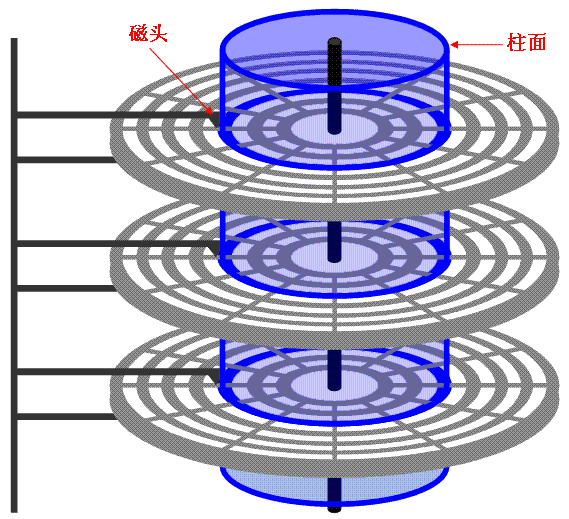
cylinder

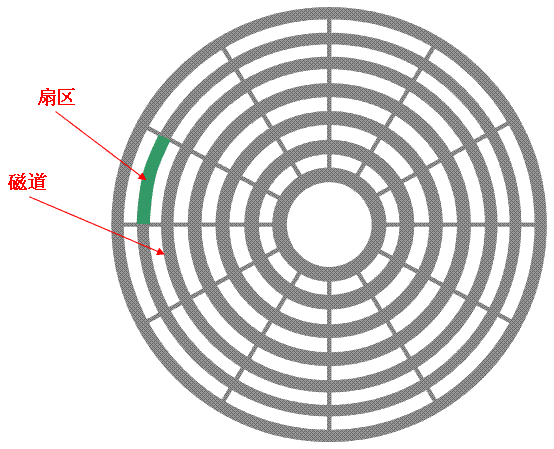
cylinder2

一图胜千言，我看书上的文字描述，一直没搞懂柱面是什么，看了上面的两张图才恍然大悟。

顺便说一下《操作系统教程》这本书就是 shit ，出到第五版还是这个样子，而且还有错别字，算式也有错的。当然，这并不能限制我去读 CSAPP。

用一句话说就是：一个盘有两个盘面，分别对应两个磁头；垂直方向上同一半径的磁道组成一个柱面；水平方向上把一个盘面等分成多个扇区。

要访问一个文件，我们需要三个参数，即：柱面号、磁头号、扇区号。

硬盘需要根据柱面号控制移动臂做横向机械运行，带动磁头到指定的柱面。我们都知道机械运动是很慢的，所以在一系列的磁盘访问中，如果可以减少磁头移动的距离，就可以减少读取的总时间。为此诞生了很多算法：FCFS，最短查找时间优先算法、扫描算法、分步扫描算法、循环扫描算法、电梯算法。

接下来，就是今天的主角：电梯算法，将会用自然语言，流程图，C++语言分别进行描述。

自然语言描述

电梯算法在无访问请求时移动臂停止不动，有访问请求时，移动臂按电梯规律移动。这里我们假设**磁盘柱面号通常由外向里递增。**每次总是选择沿移动臂的移动方向最近的那个柱面。如果当前移动方向上没有但相反方向有访问请求时，就改变移动臂的移动方向然后处理所遇到的最近的I/O请求。我们来看下面的例子，这个例子会贯穿整篇文章：

假设硬盘有 200 个柱面，编号从 0 到 199 ，有如下的访问序列： 150 30 190 20 100 55 90 当前磁头处于 50 号柱面，并且正在向内移动。

使用电梯算法移动的次序为：55 90 100 150 90 30 20，移动的总柱面数为 310。

流程图

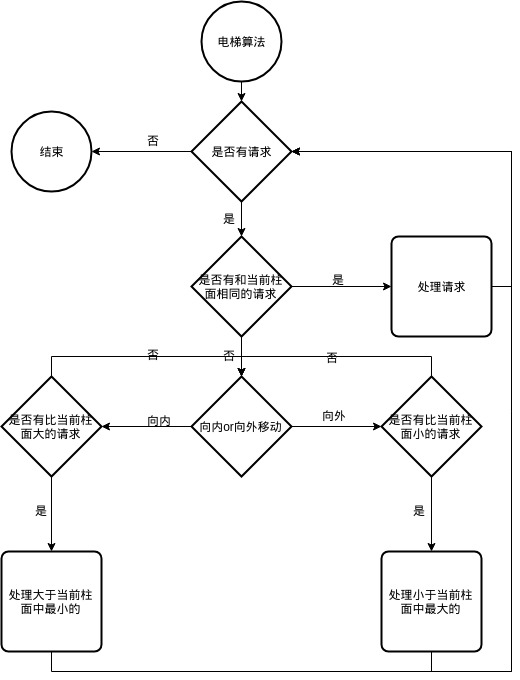
电梯算法的流程图如下：

画图工具：draw.io

电梯算法

C++

有了自然语言描述和流程图，编码的实现相对变得简单了些。这里我模仿 ACM 竞赛题的格式，把电梯算法改造成一道题目，一起来 AC 吧（

假设磁盘柱面编号由外向内递增，从0开始编号

输入格式：

第一行分别为：磁盘的柱面总数N，当前处于的柱面cur，当前移动的方向dir（1表示向内，-1表示向外）

第二行为请求访问的柱面个数n

接下来访问柱面的次序。

输出格式：

访问柱面的次序和移动臂移动的柱面总数。

输入样例：

1
2
3

200 50 1
7
150 30 190 20 100 55 90

输出样例：

1
2

55 90 100 150 190 30 20
310

需要对访问的序列进行搜索，判断是否和当前所在的柱面相同，可以用二分法加快搜索速度。接下来根据它的移动方向，判断是否有比当前柱面大或这小的柱面，有的话就去处理大于当前柱面中最小的或者是小于当前柱面中最大的。这样可以一次性处理完同一个方向的请求，并且不会有重复的移动。

main 函数代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

const int maxn = 1000;
int N, n;
int order[maxn], ans[maxn];
int cylinder[maxn] = {-1};

int main() {
  int cur, dir;
  cin >> N >> cur >> dir >> n;

  for (int i = 0; i < n; i++) {
    cin >> order[i];
  }

  sort(order, order + n);
  int sum = 0, cur_order = 0;
  while (cur_order < n) {
    int index = find_same(cur);
    if (index != -1) {  // find same
      cylinder[order[index]] = 1;
      ans[cur_order++] = order[index];
    } else {
      index = find_greater_less(cur, dir);  // find greater or less
      if (index != -1) {
        sum += (abs(order[index] - cur));
        cylinder[order[index]] = 1;
        ans[cur_order++] = order[index];
        cur = order[index];  // change cur
      } else {
        // change dir
        dir = -dir;
      }
    }
  }

  print_order(ans);
  cout << sum << endl;
  return 0;
}

使用一个cylinder 数组来标记这个柱面是否已经访问过了，在二分查找时，如果这个柱面已经访问过了，就不记录。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

/**
 * @brief  find the index of current cylinder,
 * if there is no same, return the
 */
int find_same(int cur) {
  int L = 0, R = n - 1;
  while (R - L >= 0) {
    int m = (L + R) / 2;
    // order[m] 没有被访问并且和当前柱面相同
    if (order[m] == cur && cylinder[order[m]] != 1) {
      return m;
    } else if (order[m] > cur)
      R = m - 1;
    else
      L = m + 1;
  }
  return -1;
}

对于查找大于当前柱面中最小的或者是小于当前柱面中最大的，我直接使用了顺序查找，应该也可以使用二分法来查找，但我没有过多的去优化这个实现。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

int find_greater_less(int current, int dir) {
  if (dir == 1) {  //向内,查找大于当前柱面中最小的
    // 从小到大搜索
    for (int i = 0; i < n; i++) {
      if (current < order[i] && cylinder[order[i]] != 1) {
        return i;
      }
    }
  } else if (dir == -1) {  //向外，查找小于当前柱面中最大的
    // 从大到小搜索
    for (int i = n - 1; i >= 0; i--) {
      if (current > order[i] && cylinder[order[i]] != 1) {
        return i;
      }
    }
  }
  return -1;
}

运行结果和书上的一致：

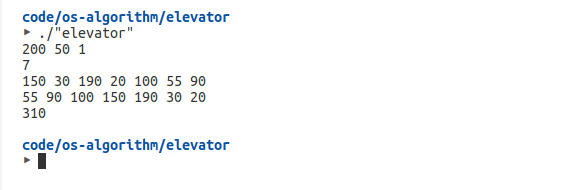
elevator-result

所以总的来讲我实现的电梯算法的时间复杂度是O(n^2)，但是我觉得可以优化到O(nlgn)，等我考完试再说。。。

参考