扫雷游戏中的算法：Union Find 和 Flood Fill

讲讲我在实现扫雷游戏时用到的算法，包括 Knuth shuffle、Union Find 和 Flood Fill。

可以在GitHub下载体验，Emoji Mines 是一年前就完成的作品。今天把雷生成的算法改了改，游戏体验变好许多，遂又向女胖友推销自己游戏（笑

在阅读之前假设你已可以熟悉扫雷的游戏规则。为了方便描述，将扫雷游戏中的方块分为：空白方块（即周围都没有雷方块的方块）、数字方块和雷方块。

雷的生成

雷的生成要保证随机，游戏体验才会好。游戏刚开始的阶段，也可以快速标记雷的位置。

替换法

替换法也就是把一个方块随机替换为雷，知道所有雷都放置完成。但是实际玩耍起来，体验不是很好，根本看不出哪个是雷，全靠盲猜。这样肯定要怀疑这个算法（特指下面实现方法）的随机性的，也不知道是不是Random的锅。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


  private void genRandomMines(int mineSize) {
    Random random = new Random(System.currentTimeMillis());
    while (mines.size() != mineSize) {
      // [0, 63]
      int nextMine = random.nextInt(size * size);
      Point point = oneD2point(nextMine);
      if (!mines.contains(point)) {
        board[point.x][point.y] = true;
        mines.add(point);
      }
    }
  }

洗牌法

然后一年过去，在知乎上偶然看到关于雷生成的算法，里面提到了洗牌法（shuffle）。使用的是 Knuth shuffle ，简单的说就是遍历数组，随机交换两个元素：

1
2
3


for i from 0 to n−2 do
     j ← random integer such that i ≤ j < n
     exchange a[i] and a[j]

洗牌法分为两步：

首先将雷按序填入游戏地图
再使用 Knuth shuffle 打乱顺序

为了更好的游戏体验，下面算法可以实现第一次点击时，不会碰到雷。不过这也意味着雷的生成要推迟到第一次点击时。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26


   // ensure excludePoint is not mine
	private void genRandomMinesEnsured(int mineSize, Point excludePoint) {
    // fill mines
    int minesCnt = 0;
    for (int i = 0; i < size; i++) {
      for (int j = 0; j < size; j++) {
        if (i == excludePoint.x && j == excludePoint.y) continue;
        board[i][j] = true;
        minesCnt++;
        if (minesCnt == mineSize) break;
      }
      if (minesCnt == mineSize) break;
    }
    // shuffle array
    Random random = new Random(System.currentTimeMillis());
    for (int i = 0; i < size; i++) {
      for (int j = 0; j < size; j++) {
        int randomPoint = random.nextInt(size * size);
        Point point = oneD2point(randomPoint);
        if (i == excludePoint.x && j == excludePoint.y || point.equals(excludePoint)) continue;
        boolean temp = board[point.x][point.y];
        board[point.x][point.y] = board[i][j];
        board[i][j] = temp;
      }
    }
  }

空白区域

当点击空白方块，会连带出所有连通的空白方块和周围的数字方块。如下图所示：

这里有两种算法可以选择，也就是文章题目中的：Union Find 和 Flood Fill 。

Union Find

使用 Union Find 来实现连带空白方块是我最初的想法。在学习 Union Find 这个算法的时候，就想到：“诶，这个好像可以用在扫雷里吧”。之后，用了一晚上的时间写出了使用 Union Find 实现的扫雷。也是第一次觉得算法还是有用的（

Union Find API

初始化，每个节点各自成一个连通块：
1
2
3
for (int i = 0; i < n; i++) {
	parent[i] = i;
}

union：连接两个连通块。将两个节点设置为同一个root。

1
2
3
4
5
6
7


    public void union(int p, int q) {
        int rootP = find(p);
        int rootQ = find(q);
        if (rootP == rootQ) return;
        parent[rootP] = rootQ;
        count--;
    }

connected：判断两个连通块是否相连。相同root的两个连通块就是连通的。

1
2
3
4
5
6
7
8
9


    public int find(int p) {
        validate(p);
        while (p != parent[p])
            p = parent[p];
        return p;
    }
    public boolean connected(int p, int q) {
        return find(p) == find(q);
    }

应用到扫雷游戏

我们可以利用union操作将全部空白方块合成一个连通块，到我们点击到一个空白方块时，遍历游戏地图，将与其连通的空白方块都显示出来。因为游戏地图为二维数组，需要将二维坐标转化为一维坐标。

联合所有空白方块：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26


  private void unionAllBlankBlock() {
    //as known, [i, j] is already a blank.
    for (int row = 0; row < size; row++) {
      for (int col = 0; col < size; col++) {
        if (isBlank(row, col)) {
          int thisPoint = xyTo1D(row, col);
          // top
          if (isBlank(row - 1, col)) {
            unionUF.union(thisPoint, xyTo1D(row, col));
          }
          // left
          if (isBlank(row - 1, col)) {
            unionUF.union(thisPoint, xyTo1D(row - 1, col));
          }
          // bottom
          if (isBlank(row, col + 1)) {
            unionUF.union(thisPoint, xyTo1D(row, col + 1));
          }
          // right
          if (isBlank(row + 1, col)) {
            unionUF.union(thisPoint, xyTo1D(row + 1, col));
          }
        }
      }
    }
  }

显示和当前空白方块相连的空白方块：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


  private void showUnionBlankBlock(Point point) {
    if (isFirstTimeBlankClick) {
      unionAllBlankBlock();
      isFirstTimeBlankClick = false;
    }
    for (int i = 0; i < size; i++) {
      for (int j = 0; j < size; j++) {
        // 判断是否相连
        if (unionUF.connected(xyTo1D(point.x, point.y), xyTo1D(i, j))) {
          Point p = new Point(i, j);
          // 显示空白方块
          setBlankBox(p);
          // 显示周围的数字
          showNumberAroundBlank(i, j);
          clearFlag(p);
        }
      }
    }
  }

Flood Fill

Flood Fill（平铺算法？）其实就是个DFS，递归遍历四连通的方块，并将其标记。同样可以用来连带出所有连通的空白方块。

因为我的游戏已经使用 Union Find 实现，而且自己当时写的代码扩展性较差，如果要换算法，大概要全部重写。所以这里用一个简单的例子介绍 Flood Fill 算法。

假设有游戏地图如下：

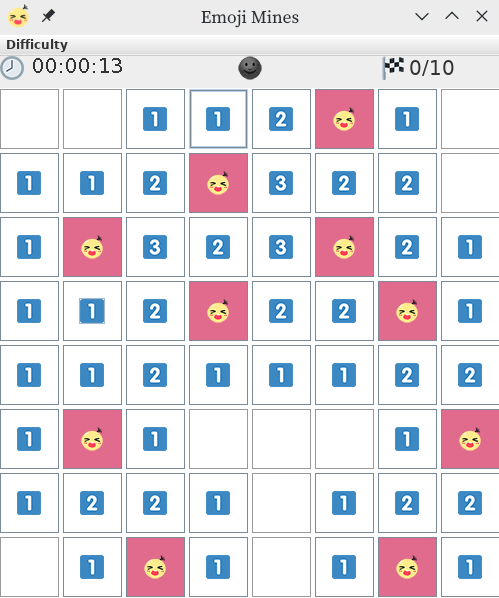
flood-fill-example

当我们点击坐标(5, 4)时，可以连带出5个空白方块组成的连通块（下方的T型）。

这个游戏地图用二维数组表示，把雷用“9”表示，因为一个方块周围最多有8个雷；已经展示的空白方块用“10”表示，防止重复遍历。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


    int[][] board = new int[][]{
        {0, 0, 1, 1, 2, 9, 1, 0},
        {1, 1, 2, 9, 3, 2, 2, 0},
        {1, 9, 3, 2, 3, 9, 2, 1},
        {1, 1, 2, 9, 2, 2, 9, 1},
        {1, 1, 2, 1, 1, 1, 2, 2},
        {1, 9, 1, 0, 0, 0, 1, 9},
        {1, 2, 2, 1, 0, 1, 2, 2},
        {0, 1, 9, 1, 0, 1, 9, 1}
    };

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


  public void floodFill(int[][] board, int x, int y) {
    if (x < 0 || x >= rows || y < 0 || y >= cols) return;
    if (board[x][y] != 0) return;
    // show blank box
    board[x][y] = 10; // showed
    System.out.printf("show blank: (%d, %d)\n", x, y);
    showNumberAroundBlank(board, x, y);
    // DFS right, left, up, down
    floodFill(board, x + 1, y);
    floodFill(board, x - 1, y);
    floodFill(board, x, y + 1);
    floodFill(board, x, y - 1);
  }

输出如下：

1
2
3
4
5


show blank: (5, 4)
show blank: (6, 4)
show blank: (7, 4)
show blank: (5, 5)
show blank: (5, 3)

使用哪个算法

首先还是推荐使用 Flood Fill 算法，因为它更加适合这个场景，实现简单。

使用 Union Find 我们还要进行坐标转化、额外的存储空间、连带时需要遍历整个地图。所以整个连带操作的时间复杂度为O(row*col*lg(row*col))。

Contents