• 二叉树的第 i 层最多有$2^{i-1}$个节点

  • 深度为 h 的二叉树最多有$2^h - 1$个节点。定义根节点深度为1。

  • $n_0$(度为 0 的节点，叶子节点)，$n_1$（度为 1 的节点），$n_2$（度为 2 的节点），有 $n_0 = n_2 + 1$

1
2
3

n0+n1+n2-1 = 0*n0+1*n1+2*n2

n0 = n2+1

分类

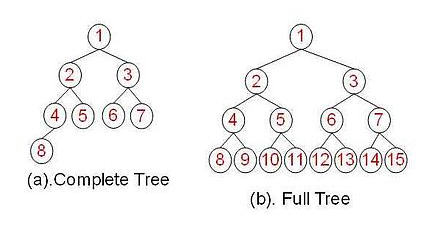
完全二叉树和满二叉树

完全二叉树 满二叉树
描述 除了最后一层其余都是满的。 满足最多的节点数。
树高 $h = lgk +1$ $h = lg(k + 1)$
节点数 $2^{h-1} \le k \le 2^h - 1$ $2^h -1$

应用

二叉树可以实现二叉树和二叉搜索树，用于排序和搜索。

  • 二叉堆（Binary Heap）：一棵完全二叉树，并且父节点的值都大于等于子节点的值。
  • 二叉搜索树（BST）：symmetric order的二叉树，即左子树的全部值 < 父节点 < 右子树的全部值 。

二叉树的遍历

二叉树的遍历用递归实现代码十分简介，因为树结构就是递归定义的。

前序遍历

根节点 -> 左孩子 -> 右孩子

1
2
3
4
5
6
7
8

  private void preOrder(TreeNode root) {
    if (root == null) {
      return;
    }
    preOrderList.add(root);
    preOrder(root.left);
    preOrder(root.right);
  }

中序遍历

左孩子 -> 根节点 -> 右孩子

1
2
3
4
5
6
7
8

  private void inOrder(TreeNode root) {
    if (root == null) {
      return;
    }
    inOrder(root.left);
    inOrderList.add(root);
    inOrder(root.right);
  }

后序遍历

左孩子 -> 右孩子 -> 根节点

1
2
3
4
5
6
7
8

  private void postOrder(TreeNode root) {
    if (root == null) {
      return;
    }
    postOrder(root.left);
    postOrder(root.right);
    postOrderList.add(root);
  }

层次遍历

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

  private Queue<TreeNode> levelOrderQueue = new LinkedList<>();
  private ArrayList<TreeNode> levelOrderList = new ArrayList<>();
  // Just likes BFS, and preOrder, inOrder and postOrder are like DFS
  private void levelOrder(TreeNode root) {
    levelOrderQueue.add(root);
    while (!levelOrderQueue.isEmpty()) {
      TreeNode node = levelOrderQueue.poll();
      levelOrderList.add(node);
      if (node.left != null) levelOrderQueue.add(node.left);
      if (node.right != null) levelOrderQueue.add(node.right);
    }
  }

相关面试题

验证二叉搜索树的后序遍历序列

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。假设输入的数组的任意两个数字都互不相同。

  • 思路：二叉树的后序遍历后，根节点肯定在数组最后。根据 BST 的性质左子树 < 父节点 < 右子树。首先找到左子树的位置，把序列分成两段，前一段都小于根，后一段都大于根。 这两棵子树也符合这样的定义。也就是递归定义，可以用递归解决。

  • 代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

public class Solution {
  private boolean valid(int[] squence, int start, int end) {
    if (start >= end) return true;
    int p = end;
    // find the left tree & valid right
    while (p > start && squence[end] < squence[p - 1]) p--;
    // valid left
    for (int i = p - 1; i >= start; i--) {
      if (squence[i] > squence[end]) return false;
    }
    return valid(squence, start, p - 1) && valid(squence, p, end - 1);
  }

  public boolean VerifySquenceOfBST(int[] sequence) {
    if (sequence.length == 0) return false;
    return valid(sequence, 0, sequence.length - 1);
  }
}

参考